Lens Maker

Optics is fascinating. There is a lot of theory too.

In order to better understand ophtalmic lenses, I built a simulator to see the influence that various design parameters have on the final result. Each parameter influence is reflected (no pun intended) in real time into the lens design, so that its impact can be immediately appreciated.

The simulator has been used to provide the parameters to model the -3 diopter lens in the following image:

The following parameters need to be put in as an imput and can be moved to alter the lens design:

• lens power : the overall power of the lens in diopters, according to the prescription. For example I have myopia and i am missing 3 diopters, so the overall power required by my lens will be -3 diopters.

• Lens base curve : this is the curve on the opposite side of the eye. It defines the overall front curvature of the glasses and how much they “wrap” around the face. Given a specific lens power, there are two optimal base curves that produce a lens with minimum astigmatic aberrations. The Tscerning Ellipse, and in particular the lower half of it, gives the optimal combination.

• Material refractive index : the ratio of the speed of light in air and the speed of light in the material, which affects the way light is bent when it enters and exits the material according to Snell’s law.

• Lens diameter : the larger the lens, the thicker it will be at its edges. Typically lens blanks for spectacles range from 4 cm to 7.5 cm, depending on the frame shape and the center of vision.

• Lens center thickness : thinner lenses have the minimum possible center thickness allowed by the material strength and by the manufacturing technology.

From the five above parameters the simulator draws the lens section, which can be replicated in a CAD program like in the following Fusion sketch:

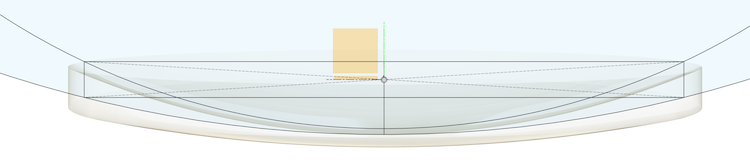
The following parameters are calculated analitically by the simulator:

• back power: the power of the lens in diopters, following that the resulting power equals the front plus back powers, i.e. P = F + B.

• Front radius: the radius of the circumference which defines the front surface of the lens. A positive value means that the surface is convex and that the center of the circumference is left of the center axis. A negative value, conversely, means that the center is right of the center axis and that the surface is concave.

• Back radius: the radius of the circumference which defines the back surface of the lens. A positive value means that the surface is convex and that the center of the circumference is right of the center axis. A negative value, conversely, means that the center is left of the center axis and that the surface is concave.

• Edge Thickness: the shape of the lens is defined by the resulting thickness, which is an important parameter for the overall aesthetics of the lens, weight and bulkiness of the final outcome. Thinner lenses can be achieved by selecting a highly refractive material or by limiting the frame size. Aspheric lenses can also be an option, but I have still not found the theory source to provide a simulator.

The last three parameters, in particular, are the ones needed to model the lens section sketch of the previous figure.

And finally, here is the simulator, it has been fun to code it. Let me know if you use it in the comments below.